En el camino hacia nuevas dimensiones.
Una segunda solución existe, introducir dimensiones suplementarias. Veamos por qué. Lo que es fastidioso en el fondo es que la masa de Planck sea muy grande. ¿Entonces por qué no hacer bajar esa masa de Planck?
Esto puede parecer una completa locura, ya que después de todo, la masa de Planck únicamente depende de la velocidad de la luz c, de la constante de Planck h y de la constante de la gravitación G, constantes universales precisamente. Paciencia, sigamos inicialmente la idea de Dimopoulos, Dvali, Arkani-Hamed en 1998 que partieron de la teoría de las supercuerdas.
Como siempre en física fundamental, las leyes emanan de un principio de menor acción. No es vital para el lector el saber lo que esto significa para comprender la continuación del artículo. Todo lo que hay que saber, es que existe una cantidad bautizada acción de Einstein-Hilbert y lo que se anota a SEH y que permite derivar las ecuaciones de Einstein del campo de gravitación. Se escribe:
Donde R4 es el escalar de curvatura 4d del espacio tiempo (obtenido por contracción del tensor de Riemann) y G4, nuestra buena vieja constante de la gravitación en dimensión 4. La acción de Einstein Hilbert se calcula haciendo una suma íntegra sobre un campo del espacio tiempo a cuatro dimensiones.
Cuando se busca unificar las interacciones con la gravitación, una estrategia es aumentar el número de dimensiones del espacio, como en los casos de las teorías de Kaluza-Klein y de las supercuerdas. Podemos entonces derivar las ecuaciones de Einstein en n dimensiones inmediatamente con SEH sumando en un volumen de espacio tiempo a n dimensiones.
Más precisamente, añadamos p dimensiones suplementarias tales como p+4=n, tendremos entonces
Donde Rn es siempre el escalar de curvatura pero en n dimensiones y Gn la constante de la gravitación en un espacio-tiempo en n dimensiones.
Y si integramos entonces obtenemos como resultado aproximado:Mágicamente, lo que tomo por la "verdadera" constante de gravitación 4d es de hecho la constante exacta nd corregida por un factor de volumen Vp que proviene de dimensiones suplementarias.
Finalmente, la verdadera constante de la gravitación Gn en n dimensiones es dada por:
Si se utiliza el cuadrado de la masa de Planck Mpl habitual en 4 dimensiones, la verdadera masa de Planck Mn en n dimensiones deviene entonces (si se coloca h=c=1 en un sistema de unidades apropiado).
¡La solución salta a la vista!.
Si Vp tiene suficientemente grande la escala de gran unificación está entonces alrededor de 1 Tev y todo vuelve a la normalidad sin suponer la supersimetría.
¡Además, esto querría decir que toda la física de la Gran Unificación y de la gravedad cuántica podría ser accesible al LHC!
Raman Sundrum
© TASI
(pulsar sobre la imagen para ampliarla)
Existe otro enfoque del problema de la jerarquía que utiliza también dimensiones suplementarias pero que no presupone que la teoría de las cuerdas sea verdadera. Descansa en el modelo de geometría deformada* con una dimensión suplementaria y es conocida de hecho desde los años 1980 en la teoría de supergravedades de Kaluza-Klein.
Ha sido propuesta en 1999 por Lisa Randall y Raman Sundrum. Consiste en tomar las ecuaciones de la gravitación de Einstein 5d (Kaluza-Klein) para describir dos universos paralelos en 4 dimensiones separados por una distancia débil que se extiende según la quinta dimensión. La métrica de espacio-tiempo que sirve para medir las distancias en tal Universo, una generalización del teorema de Pitágoras de la forma siguiente:
Donde y se corresponde a una quinta coordenada espacial.
Introduciendo esta métrica en el escalar de curvatura precedente de la acción de Einstein-Hilbert, casualmente, recaemos sobre la situación descrita anteriormente. Todo cálculo hecho en íntegrales similares a la precedente encontramos un factor V que depende de f(y) y que puede ser también grande.
En ambos casos, la masa de Planck podría ser de 1 TeV pero de hecho, nada la obliga allí, podría además ser de 1.000 TeV. Tomarla igual a algunos TeV es sólo uno de los modos eliminar el problema de la jerarquía de modo elegante, pero nada nos prueba que la Naturaleza hubiera escogido este modo de proceder.Lisa Randall
© Matthew J. Lee
(pulsar sobre la imagen para ampliarla)
Debería ser posible fabricar mini agujeros negros.
Seamos optimistas y tomémosla igual a 5 TeV. ¡En estas condiciones, si dos partículas que poseen una energía E superior a esta masa de Planck chocan y en un volumen cuyo radio es inferior al radio de Schwarzschild Rs=2GM/c2 dado por el equivalente en masa M=E/c2 de esta energía, un mini agujero negro se formará en seguida!
Los primeros en contemplar esta posibilidad fueron Tom Banks y Willy Fischler en 1999. Este artículo precursor contemplaba claramente que tal mini agujero negro debía evaporarse muy rápidamente a causa del efecto Hawking pero habrá que esperar al impacto de los artículos de Steven Giddings y Savas Dimopoulos en 2001 para que los primeros cálculos un poco detallados de este escenario fueran publicados y llamaran la atención de una amplia parte de la comunidad científica.
Muy rápidamente, los dos artículos de 2001 dieron lugar a otros más explorando no sólo la posibilidad de crear mini agujeros negros en el LHC sino también de observarlos en las colisiones de los rayos cósmicos de altas energías que caían sobre la Tierra, con instrumentos en el suelo como Auger e IceCube. El debate también hizo furor sobre los fundamentos de los cálculos de producción de mini agujeros negros a energías superiores a la energía asociada con la nueva masa de Planck, así como sobre la observabilidad de la radiación Hawking de estos mini agujeros negros.
Steven Giddings explicando la teoría del Paisaje cósmico (Landscape) con una superficie de Riemann.
© Richard Harris, NPR
(pulsar sobre la imagen para ampliarla)
Es en ese contexto que se inscriben los trabajos de Aurélien Barrau y sus colegas, entre los que se encuentran Julien Grain y Stanislas Alexeyev. Futura-Sciences le pidió al laureado con el Premio Bogoliubov 2006 si podía hablarnos más sobre el posible descubrimiento de mini agujeros negros en el LHC. Habiéndose generado tanta polémica en Internet respecto a los supuestos riesgos de un fin del mundo arrastrado por tales objetos, le pedimos desde luego lo que pensaba sobre eso. Generosamente dedicó parte de su tiempo para responder a todas nuestras cuestiones durante una entrevista, la cual podrán leer en un próximo artículo.
Para saber más:
La teoría de cuerdas no es capaz de describir un mundo de tres dimensiones. Sugiere un mundo con muchas más dimensiones, nueve o diez. Raman Sundrum y otros, han demostrado por qué en un mundo con una dimensión adicional espacial, la gravedad sería tan débil. Su idea se basa en una geometría deformada, que surge a partir de la teoría de la relatividad general de Einstein. Según esa teoría, el tiempo y el espacio están integrados en una única estructura espacial-temporal distorsionada, o deformada, por la materia y la energía. Aplicamos esta teoría en un contexto de dimensiones adicionales y encontramos una configuración en la cual el espacio-tiempo se deforma tanto que aunque la gravedad fuera fuerte en una región del espacio sería endeble en otra. El universo de la propuesta es un multiverso: la gravedad está en un universo y nosotros en otro, separado por una cuarta dimensión espacial.
Todos los capítulos:
- Intentando aclarar dudas
- En el camino hacia nuevas dimensiones
- Entrevista a Aurélien Barrau (1ª parte)
- Entrevista a Aurélien Barrau (2ª parte)
Agradecimientos (para toda la serie): Wikipedia. IIEH. Eduardo J. Carletti.
Traducido para Astroseti.org por Xavier Civit
Enlace: http://www.futura-sciences.com/
Vía: Astroseti

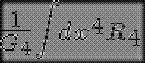
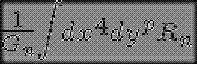
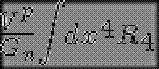
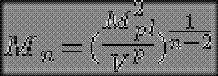







 Imagen actualizada por la USNO
Imagen actualizada por la USNO







0 comentarios:
Publicar un comentario
Todos los comentarios son responsabilidad únicamente de sus autores y no refleja necesariamente el punto de vista de este sitio.
NO insultes a nadie.